kann mir jeamnd sagen wie ich hier vorgehen muss? mache ich das mit den formeln: kp= up(t1)/ e(t1) oder durch grafisches ableiten?
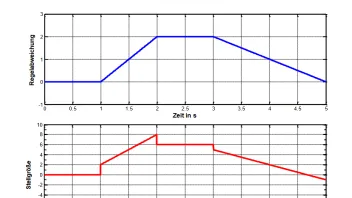
kann mir jeamnd sagen wie ich hier vorgehen muss? mache ich das mit den formeln: kp= up(t1)/ e(t1) oder durch grafisches ableiten?

Hi, das kannst du eigentlich grafisch lösen.
Jetzt am Beispiel von t=1s:
- D-Anteil: da haben wir eine Änderung in der Steigung, die 2 ist, wodurch du schonmal k_d*e' = 2 hast. Da die Steigung sich bis t=2 nicht ändert, bleibt die Wirkung erhalten.
- Dazu kommt noch der P-Anteil: da die Abweichung linear zunimmt, muss auch die Stellgröße gleichermaßen, aber mit dem Faktor k_p multipliziert zunehmen.
- Und bei t=2 ist die Steigung in der Regelabweichung 0, wodurch der anhebende D-Anteil verschwindet.... so kannst du weitermachen.
LG
kannst du viellcheit das mit k_d*e' = 1 und wie ich den p teil drrauf amche genauer erklären, habe es jetzt so zu 50% verstanden
e ist ja einfach die Regelabweichung.
Dieses kannst du, für den P Anteil dem ersten Diagramm direkt entnehmen und mit k_p (also 3) multiplizieren.
Für den D-Anteil: musst du noch die Steigung von e (Steigung von e = e')ablesen, welches zwischen t=1 und t=2, einfach 2 ist.
Damit ergibt sich die Stellgröße zwischen t=1 und t=2 zu: u = k_p * e + k_d * e'
Das trägst du dann im 2. Diagramm ein.
e: wird in dem Intervall größer
e' bleibt konstant 2
Sorry hatte vorhin e'=1 gesagt, da habe ich falsch abgelesen

