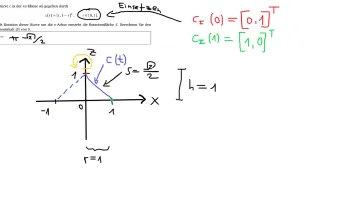
Hallo, kann mir jemand sagen wie ich diese aufgabe lösen kann? meine vermutung ist der Ansatz: |S| = 2π ∫ x = 2πxs · |c|. Komme mit diesem ansatz keider auf was komisches, nämlich auf 4/3πt·√2.
Das wäre die aufgabe, meine vermutung ist, dass es was simples sein muss, da es nur eine fill aufgabe ist.