Weiß jemand wie man diese Aufgabe bzw. diesen Aufgabentyp löst?
Danke 
WS 2016 Aufgabe 2f
-
Ich weiß zwar nicht, ob es die schnellste Möglichkeit ist, aber man kann erst nach dy integrieren (Subst. 1 Art dann partielle Integration) und dann den Term wieder nach x ableiten. Schau dir die Integration bzw. Ableitung auf Ableitungsrechner.net an, falls du Probleme hast.
-
Mann muss doch hier beim Integrieren nach y doch gar nicht Substitution machen, sondern lediglich per part. Int arctan integrieren.
Wird hier nicht das x^2 in der Klammer einfach als Konstante gesehen bei der Int nach y ?
-
ja, allerdings ist arctan(constante*x) ja was anderes als arctan(x) und somit können Fehler entstehen. Mit der Substitution macht man da keine Fehler (ohne muss man sich merken, was sich verändert)
-
- Offizieller Beitrag
Es ist bei diesem Aufgabentyp nicht nötig die Funktion g(x,y) im Integral zu integrieren - Substitution hin oder her, die Stammfunktion des Arctan ist nicht angenehm. Man darf Integral und Ableitung einfach vertauschen.
Es gilt:
Der Inhalt kann nicht angezeigt werden, da Sie keine Berechtigung haben, diesen Inhalt zu sehen. Konkret auf dieses Beispiel heißt das, dass man erst
nach dx ableitet und danach nach dy in den Grenzen [0,1] integriert, anstatt erst nach dy zu integrieren und danach nach dx zu differenzieren. Für die Ableitung nach dx erhalte ich bei mirDer Inhalt kann nicht angezeigt werden, da Sie keine Berechtigung haben, diesen Inhalt zu sehen. . Das Integral nach dy ergibt sich dann zuDer Inhalt kann nicht angezeigt werden, da Sie keine Berechtigung haben, diesen Inhalt zu sehen. .Der Inhalt kann nicht angezeigt werden, da Sie keine Berechtigung haben, diesen Inhalt zu sehen. Ich hoffe mein Rechenweg ist verständlich und nachvollziehbar. Mein Ergebnis stimmt mit dem aus der Filebase Mathematik II < Musterklausuren < WiSe 16/17 Lösungen ohne Rechenweg überein …
-
Wenn man zuerst Ableitet und dann nach dy integriert, da kriegt man ja als Stammfunktion ln(u) raus mit der unteren grenze 0 und der obere grenze x^4+1. Ist das Integral dann nicht definiert, da man 0 nicht in ln einsetzen kann?
-
Du musst auch die Grenzen mit transformieren bei Substitution. Ich habe x^4y^2+1=u gesetzt und wenn ich hier meine Grenzen einsetze komme ich auf ein Intervall von 1 - x^4+1 und damit hast du keine Probleme und kommst auf das oben stehende Ergebnis.
-
- Offizieller Beitrag
Bei dem Integral kann man sich mit einem kleinen Trick behelfen:
.Der Inhalt kann nicht angezeigt werden, da Sie keine Berechtigung haben, diesen Inhalt zu sehen. Wenn man mit 1 = x^3/x^3 erweitert ergibt sich
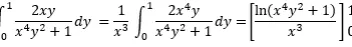. Da x im Integral nach dy eine Konstante ist kann man den x-Term, welcher unabhängig von y ist, vor das Integral ziehen.Man kann bei der Stammfunktion ohne Probleme y = 0 einsetzten, da man in dem Fall ln(0*x^4 + 1) = ln(1) = 0 erhält. Damit wird auch der Wert der gesamten unteren Grenze zu 0.
Vielleicht ist das nun etwas klarer …
