Soweit ich weiß ist das Kapitel nicht relevant
Korrekt.
Soweit ich weiß ist das Kapitel nicht relevant
Korrekt.
SS 16 Aufgabe 1 e)
Kann mir bitte jemand erklären, wie man auf die Wurzel von beta_2 kommt? Setzt man t* ein, und löst nach beta_2 auf, seh ich keinen Schritt zum quadrieren/Wurzel ziehen...

Kann mir bitte jemand erklären, wie man auf die Wurzel von beta_2 kommt?
Bei der vorletzten Gleichung die Klammer auflösen. Dann hast du (beta_2)^2.
Danach einfach nach (beta_2)^2 umformen und Wurzel ziehen.
Bei der vorletzten Gleichung die Klammer auflösen. Dann hast du (beta_2)^2.
Danach einfach nach (beta_2)^2 umformen und Wurzel ziehen.
ok, ich bin blind.. danke!
WS16/17 Aufgabe 2c)
Weiß jemand wie man auf auf die Kontaktbedingung für den Kontakt K2 kommt? Beziehungsweise nach welchem Schema werden die Kontaktbedingungen von K1 und K2 formuliert? K1 erscheint mir ja noch recht logisch aber K2 hätte ich komplett anders formuliert

Ich hätte mal eine andere Frage. In einem alten Beitrag habe ich gelesen, dass es keine Folgefehler gibt. Heist es, wenn ich bspw. die Eigenvektoren in Aufgabenteil b) falsch ausgerechnet habe und anschließend in der c) die modale Massenmatrix M ausrechne, dass ich 0 Punkte für c) bekomme?
WS16/17 Aufgabe 2c)
Weiß jemand wie man auf auf die Kontaktbedingung für den Kontakt K2 kommt? Beziehungsweise nach welchem Schema werden die Kontaktbedingungen von K1 und K2 formuliert? K1 erscheint mir ja noch recht logisch aber K2 hätte ich komplett anders formuliert
Woher hast du denn diese Lösung? In meiner Version steht nämlich Folgendes:

Woher hast du denn diese Lösung? In meiner Version steht nämlich Folgendes:
Ahh, vielleicht sollte ich mal nicht mir den Versionen von vor 1,5 Jahren arbeiten. Jetzt ergibt das auch Sinn, danke!
Ahh, vielleicht sollte ich mal nicht mir den Versionen von vor 1,5 Jahren arbeiten. Jetzt ergibt das auch Sinn, danke!
Für die Gelenke A,B und C konnte ich die Bindungsgleichungen aufstellen, für die Kontakte K1 und K2 blicke ich nicht so durch. Ich will ja im Grunde genommen sagen, dass die Scheibe bei K1 nicht abheben darf. Deshalb nehmen wir ja die Gleichung mal ey1. Warum muss ich hier Konstanten angeben?
Für die Gelenke A,B und C konnte ich die Bindungsgleichungen aufstellen, für die Kontakte K1 und K2 blicke ich nicht so durch. Ich will ja im Grunde genommen sagen, dass die Scheibe bei K1 nicht abheben darf. Deshalb nehmen wir ja die Gleichung mal ey1. Warum muss ich hier Konstanten angeben?
Für die gesamte Bindungsgleichung, also noch nicht ausmultipliziert, müssen die Konstanten angegeben werden. In x1-Richtung vom Schwerpunkt S1 zum Kontakt (K1 und auch K2) noch ein bestimmter Abstand ist, der durch diese Konstante angegeben wird. Sind im Prinzip irrelevant, da sich diese wegkürzen - aber ich denke, initial muss man diese erwähnen.
Für die gesamte Bindungsgleichung, also noch nicht ausmultipliziert, müssen die Konstanten angegeben werden. In x1-Richtung vom Schwerpunkt S1 zum Kontakt (K1 und auch K2) noch ein bestimmter Abstand ist, der durch diese Konstante angegeben wird. Sind im Prinzip irrelevant, da sich diese wegkürzen - aber ich denke, initial muss man diese erwähnen.
Super danke!
Dass man die benutzen muss, wusste ich auch bisher, aber ich dachte eigentlich da sie beliebig sind können Sie auch null sein und fallen deswegen weg...
Kann jemand mal eine Rechnung abfotografieren wie Konstante sich dann wegkürzt? Ich seh es irgendwie nicht...
Kann jemand mal eine Rechnung abfotografieren wie Konstante sich dann wegkürzt? Ich seh es irgendwie nicht...
So sieht die ausgeschriebene MuLö aus: 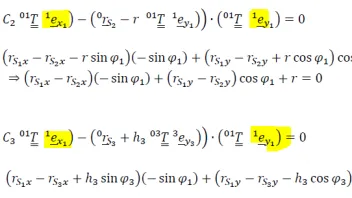
Da die Konstante für beide Kontakte nur in x1-Richtung relevant ist, und der gesamte Term am Ende mit der y1-Achse multipliziert wird (wird wie ein Schubgelenk behandelt), sieht man direkt dass die Konstante wegfällt. Die Achsen sind ja orthogonal und das Skalarprodukt damit 0.
Wenn man es ausschreibt, kommt da sowas wie C*(cos*sin - cos*sin) raus - was ja auch 0 ist.
Hallo,
bei der SoSe 17 A2 c) sollen wir die Bindungsgleichungen für alle Gelenke aufstellen. Für das Schubgelenk E hätte ich phi3 = 0 auch als eine Bindungsgleichung aufgeschrieben. Warum wird das nicht in der Lösung angegeben?
Hallo,
bei der SoSe 17 A2 c) sollen wir die Bindungsgleichungen für alle Gelenke aufstellen. Für das Schubgelenk E hätte ich phi3 = 0 auch als eine Bindungsgleichung aufgeschrieben. Warum wird das nicht in der Lösung angegeben?
E ist ein Drehschubgelenk, sodass nur eine Bindungsgleichung aufgestellt werden kann - bzgl der Schubachse. Dass das phi_3 hier 0 bleibt, ergibt sich (nur zufällig) aus der Anordnung der übrigen Gelenke/Körper.
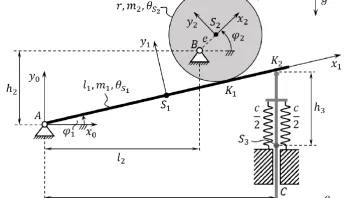
Anders beim Schubgelenk C in WS16/17 (s. Screenshot). Da ist das Schubgelenk fest und der Winkel relevant für eine der zwei Bindungsgleichungen.

Ich habe ein Frage zu SoSe 17 Aufgabe 3c. Bei der Matrix am Ende fehlt JR2T*Thetam2*JR2. (also Trägheitsmoment der Punktmasse m2 * l2. Oder wieso wird das hier ignoriert?
Ich habe ein Frage zu SoSe 17 Aufgabe 3c. Bei der Matrix am Ende fehlt JR2T*Thetam2*JR2. (also Trägheitsmoment der Punktmasse m2 * l2. Oder wieso wird das hier ignoriert?
Das kann ignoriert werden, da eine Punktmasse keine Trägheitsmomente besitzt, der Tensor wäre also 0.
Ich habe ein Frage zu SoSe 17 Aufgabe 3c. Bei der Matrix am Ende fehlt JR2T*Thetam2*JR2. (also Trägheitsmoment der Punktmasse m2 * l2. Oder wieso wird das hier ignoriert?
Das von dir erwähnte Produkt von J-Rotationsmatrix für Körper 2 ist gleich null, weil es sich bei Körper 2 um eine Punktmasse handelt. Vergleiche mal die Formeln aus der Formelsammlung für die verallgemeinerte Massenmatrix auf S.59 (Sonderfall) mit der der auf S.55 (Punktmassensystem).
Das von dir erwähnte Produkt von J-Rotationsmatrix für Körper 2 ist gleich null, weil es sich bei Körper 2 um eine Punktmasse handelt. Vergleiche mal die Formeln aus der Formelsammlung für die verallgemeinerte Massenmatrix auf S.59 (Sonderfall) mit der der auf S.55 (Punktmassensystem).
Ach eine Punktmasse hat keinen Tensor nur einen steinerschen Anteil. Das war mein Fehler oder ?
Hallo zusammen,
wie geht ihr beim Lösen des LGS für die Eigenvektoren vor? Ich hab das Gefühl ich brauch unnormal lang, und viele Rechenschritte, insbesondere bei dem vorgesehenen Platz für die Rechnung (zB. ist bei SS2016 eine Seite vorgesehen für 4 LGS) .. Irgendwelche Tipps, Tricks um da schneller voranzukommen?

